Метод дисконтирования
При оценке инвестиционного проекта часто приходится сравнивать потоки денежных средств (поступления от проекта и расходы на его осуществление) при различных вариантах его реализации. Для этого и существует дисконтирование – процедура, которая позволяет привести разновременные денежные потоки (поступления и платежи) к единому моменту времени. Чтобы такие сравнения имели смысл, денежные потоки сопоставляют в какой-то один период времени. Какой момент времени выбрать для сравнения, как рассчитать процентную ставку? – в этом на конкретных примерах поможет разобраться автор данной статьи.
Расчет показателей для оценки выгодности реального инвестирования базируется на концепции оценки стоимости денег во времени. Данная концепция исходит из предпочтительности денег сегодня, чем завтра. Многие предприниматели придерживаются этой логики, поскольку:
1. Существует риск, что деньги могут быть не получены в будущем.
2. Если деньги имеются в наличии сегодня, то их можно выгодно инвестировать для получения дохода в будущем.
В МСФО дисконтирование может повлиять на балансовую стоимость любого элемента учета и тем самым изменить финансовые результаты компании. Смысл дисконтирования заключается в том, что текущая стоимость будущих финансовых потоков может существенно отличаться от их номинальной стоимости.
Дисконтирование денежных потоков – это приведение стоимости потоков платежей, внесенных в разные моменты времени, к стоимости на текущий момент времени. Дисконтирование отражает тот экономический факт, что сумма денег, которой мы располагаем в настоящий момент, имеет большую реальную стоимость, чем равная ей сумма, которая появится в будущем. При этом применение дисконтированной стоимости денег не зависит от инфляции. Если инфляция равняется нулю, то деньги все равно будут иметь стоимость с учетом будущих доходов, которые они могут принести при инвестировании. При расчете будущей и текущей дисконтированной стоимости денежных потоков используется принцип сложных процентов.
Дисконтирование представляет собой процесс нахождения текущей величины (PV) по ее известному или предполагаемому значению в будущем (FV).
Для определения стоимости, которую будет иметь инвестиция через несколько лет, при использовании сложных процентов будущей стоимости применяется следующая формула:
FV = PV × (1 + i)n,
где:
FV – будущая стоимость инвестиции через n лет,
PV – сумма, вкладываемая в настоящий момент времени,
I – ставка процента в виде десятичной дроби 10 % = 0,1,
N – число лет в расчетном периоде.
Пример
Если мы инвестируем 200 000 тенге под 10 процентов, то какова будет стоимость инвестиций через 5 и 6 лет?
Текущая стоимость ожидаемых будущих поступлений рассчитывается по формуле:
PV = FV × (1 / (1 + i)n)
Пример
Рассчитать сумму, которую нам необходимо вложить сейчас по определенной ставке 6 процентов, для того чтобы через 4 года стоимость инвестиций составила 5 000 000 тенге.
Подставляем значения в формулу:
PV = 5 000 000 × (1 / (1 + 0,06)4) = 5 000 000 × 0,792 = 3 960 000 тенге.
Расчетные процедуры бухгалтерского учета для определения стоимости активов и обязательств основаны на принципах начисления процентов на вложенные средства.
Доход на вложенный капитал зависит от факторов:
● текущая стоимость актива – PV (Present Value)
● будущая стоимость актива – FV (Future Value)
● срока вложения – n процентной ставки – i (Interest Rate).
Полученная прибыль (I–Interest) является разницей между величиной полученных в результате финансовой операции и вложенных изначально денежных средств.
Проценты – это доход от предоставления капитала в долг либо от инвестиций производственного или финансового характера.
Различают два метода начисления процентов:
● метод исчисления простых процентов;
● метод начисления сложных процентов.
Проценты, которые применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления, называются простыми.
Ставка дисконтирования – это та процентная ставка, которую используют при приведении будущих финансовых потоков к их стоимости в настоящее время. Ее расчет, пожалуй, является одним из самых актуальных и сложных вопросов, который возникает при финансовой оценке любого инвестиционного проекта. От его корректности зависит, какую конечную величину будет иметь текущая денежная стоимость. Если применить низкую ставку, то дисконтированная стоимость ожидаемых в будущем денежных поступлений может оказаться завышенной. Это повлечет за собой выбор инвестором неэффективного проекта, в результате чего он понесет серьезные потери. Чрезмерно высокая ставка, в свою очередь, может привести к потерям, которые есть фактически, – упущенная возможность получения дохода.
Процентная ставка (i) вычисляется как отношение полученной за определенный период прибыли к величине вложенных средств, умноженных на продолжительность периода финансовой операции:
i = I / PV × n,
где:
i – процентная ставка,
I – величина дохода,
PV – сумма капитала в настоящем.
Пример
Компания приобрела за 65 000 тенге вексель, по которому через 1 год она должна получить его номинальную стоимость – 75 000 тенге. Чему равна доходность этой сделки?
По условиям примера (тенге):
FV = 75 000,
PV = 65 000.
Доход владельца векселя равен разнице между его номинальной стоимостью и ценой приобретения:
Текущая стоимость единицы (реверсии) — это величина, обратная накопленной сумме единицы. Это текущая стоимость одного доллара, который должен быть получен в будущем. Поскольку целью осуществления инвестиций является получение доходов в будущем, умножение фактора текущей стоимости реверсии на величину ожидаемого будущего дохода является важнейшим шагом в оценке инвестиций.
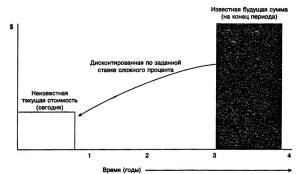
Рис. 3-6. Текущая стоимость реверсии — графическая иллюстрация
Текущая стоимость реверсии (V) описана графически на рис. 3-6. Данный коэффициент используется для оценки текущей стоимости известной (или прогнозируемой) суммы будущего единовременного поступления денежных средств с учетом заданного процента. При применении фактора текущей стоимости используются понятия дисконтирование (discounting) или ставка дисконта (discount rate), противоположные понятиям накопление (compounding) и ставка процента (interest rate), применяемым при расчете накопленной суммы единицы.
Поскольку деньги обладают стоимостью во времени, один доллар, который будет получен в будущем, стоит меньше доллара, получаемого сегодня. Насколько меньше (сумма дисконта), зависит от: а) разрыва во времени между оттоком и притоком денежных средств и б) необходимой ставки процента или дисконта.
Например, при 10%-ной ставке процента (ставке дисконта) текущая стоимость 100,00 долл., ожидаемых к получению через год, равна 90,91 долл. Арифметическая проверка: если сегодня инвестор вкладывает 90,91 долл. и в течение следующего года может получить чистый доход в 9,09 долл., то процент составит 9,09 долл.; поэтому через год основная сумма инвестиций, включая добавленный процент, будет равна 100,00 долл. (90,91 долл. + 9,09 долл. = 100,00 долл.).
Инвестор, который рассчитывает получить через два года 100,00 долл. и вкладывает сегодня 82,64 долл., получит 10%-ную годовую ставку. Проверка: при 10%-ной годовой ставке 82,64 долл. превратятся через год в 90,91 долл., а через 2 года — в 100,00 долл.
Смысл проведения подобных расчетов при работе с недвижимостью состоит в том, чтобы определить сумму, которую следует уплатить за землю сегодня с тем, чтобы перепродать ее с выигрышем в будущем. Например» инвестор, рассчитывающий перепродать собственность через 2 года за 10 000 долл., должен решить, сколько ему следует предложить эа землю сегодня. Если инвестор требует 10%-ную ставку дохода на вложенный капитал, то максимальная сумма, которую он сейчас может предложить продавцу — 8 264 долл. Более низкая цена повысит ставку дохода на инвестиции. Напротив, более высокая цена воспрепятствует достижению требуемой 10%-ной ставки дохода.
Формула расчета текущей стоимости реверсии
Формула расчета текущей стоимости реверсии имеет следующий вид:
Читатель видит, что данный фактор является обратной величиной от накопленной суммы единицы. Поэтому любая задача, которая может быть решена с использованием фактора накопленной суммы единицы, может быть также решена с применением фактора реверсии, однако не через умножение, а через деление.
Например, как показано ранее, 100,00 долл., накапливаемые по сложной ставке 10%, через пять лет возрастут до 161,05 долл. Поскольку 100,00 долл. через пять лет превратятся в 161,05 долл., то 62,05 долл. — это та сумма, которая за пять лет возрастет до 100,00 долл. Ниже показан анализ коэффициентов для данного примера:
Построение таблиц
Как и в случае с накопленной суммой единицы, регулярное и интенсивное использование в расчетах фактора текущей стоимости единицы вызвало необходимость построения стандартных таблиц. Текущая стоимость единицы приводится в колонке 4 многих таблиц сложного процента. Она рассчитывается по формуле, описанной ранее:
Поскольку это величина, обратная накопленной сумме единицы, таблицы могут быть построены соответствующим образом, как это показано в табл. 3-5:
Построение таблицы текущей стоимости реверсии (годовая ставка = 10%)
В некоторых таблицах на одной и той же странице приведены величины текущей стоимости единицы при различных ставках дисконта (процента). Такие таблицы могут быть удобны, например, для показа будущей покупательной способности 1 долл. при различных темпах инфляции. Табл. 3-6 показывает это при ставках 3, 6, 10 и 15%. Линия текущей стоимости единицы при различных ставках дисконта показана графически на рис. 3*7.
ТАБЛИЦА 3-6
Будущая покупательная способность 1,00 долл. при различных темпах инфляции
Индекс инфляции
Более частое дисконтирование
Как и в случае со сложным процентом, интервалы между периодами дисконтирования могут быть короче (более частыми), чем один год. В расчете текущей стоимости реверсии это учитывается так же, как и при накоплении процента. Номинальная ставка дисконта делится на частоту интервалов (например, при поквартальном дисконтировании делится на 4), а число периодов в году умножается на число лет.
Линии текущей стоимости при различных ставках дисконта
Применение финансового калькулятора
Для того чтобы с помощью калькулятора определить текущую стоимость известной будущей суммы, введите число временных периодов — N, периодическую ставку процента — %I и известную будущую стоимость — FV. Затем нажмите клавиши COMPUTE и PV. Дисплей покажет текущую стоимость. (На некоторых калькуляторах предварительно следует установить регистр CI.) Рис. 3-8 показывает, какие клавиши калькулятора необходимо использовать для определения текущей стоимости 10 000 долл., которые должны быть получены через пять лет при годовой ставке дисконта 10%.
Результат: 6209,21 (на дисплее)
Рис, 3-в. Клавиши калькулятора, используемые для расчета текущей стоимости реверсии при ставке дисконта 10%, ежегодном дисконтировании за 5 лет и будущей стоимости 10 000 долларов
⇐ Предыдущая123
При разработке бизнес-плана инвестиционного проекта необходимо рассчитывать ряд важных показателей, в первую очередь, таких как: чистая дисконтированная стоимость, внутренняя рента. Показатель чистой дисконтированной стоимости капитала (ЧДС — net present value) определяется сопоставлением дисконтированных на основе финансово-математического аппарата доходов (Д0) и расходов (В0):
(15)
Критерий метода чистой дисконтированной стоимости заключается в следующем: инновационный проект является выгодным при выбранной процентной ставке, если приведенная стоимость капитала больше или равна нулю:
(16)
Пpи ЧДС = 0 инвестор только возмещает свои расходы. Чем выше значение ЧДС, тем эффективнее проект. Величина чистой дисконтированной стоимости капитала зависит от размера установленной процентной ставки. Зависимость между этими показателями показана на рис. 14.
Рис. 14. Изменение дисконтированной стоимости капитала при повышении процентной ставки
В точке пересечения кривой с осью координат дисконтированная стоимость равна нулю. Значение процентной ставки в этой точке является критическим (iкр). В случае, когда i < iкр проект является выгодным. Пpи i = iкр инвестор только получит возмещение затрат. Эта точка является пределом эффективности, проект при этих условиях считается минимально эффективным. Когда і>ікр икр чистая дисконтированная стоимость имеет отрицательное значение и проект неэффективен.
На практике инвестиционные процессы могут характеризоваться числовым рядом с одинаковыми и различными ежегодными платежами. При одинаковых доходах (д) и расходах (в) численный ряд, характеризующий проект, можно представить в виде рис. 15.
Величина расходов определяется с учетом годовых производственных затрат:
, (17)
де КСДn – коэффициент суммарного дисконтирования.
0 1 2 3 4 . . . n годы
Рис. 15. Денежные потоки инновационного проекта
где – д – текущие доходы;
в – текущие затраты;
В – затраты на создание объекта;
Дл – выручка от реализации объекта.
Величина доходов определяется с учетом ежегодных доходов (Д) и ликвидационной стоимости (Дл):
(18)
Приведенная стоимость капитала при неизменных годовых платежам характеризуется следующей формулой:
(19)
Рассмотрена формула может использоваться только в случае, когда платежи (доходы, расходы) остаются неизменными. Hа практике это может иметь место при усреднении годовых расходов и доходов. Если есть отклонения от этих условий, то расчет ЧДС выполняется следующим образом.
(20)
Пример. Инвестор планирует вложить средства в новое оборудование стоимостью 420,0 тыс. д. ед. Ожидается, что его эксплуатация будет приносить ежегодно доходы 150,0 тыс. д. ед. и требует текущих расходов ежегодно 60,0 тыс. д. ед. Гарантированный производителем срок эксплуатации составляет 6 лет, после чего оборудование можно реализовать за 20,0 тыс. д. ед. Оценить целесообразность инвестирования при і = 0,08.
Рис. 16. Определение ЧДС при равномерных текущих платежах
Капиталовложения в новое оборудование выгодно, потому что 8,6626 тыс. д.ед. > 0.
Пример. Планируется освоение производства новой продукции. Доходы от реализации в течение четырех лет, будут составлять 280,0 тыс. д. ед. Затраты на производство составляют по годам:
в1 = 190,0 тыс. д. ед.,
в2 = 80,0 тыс. д. ед.,
в3 = 70,0 тыс. д. ед.,
в4 = 160,0 тыс. д. ед.
Через четыре года производственное оборудование планируется продать за 200,0 тыс. д. ед. Оценить выгодность инновационного проекта при і = 7 %.
Рис. 17. Определение ЧДС при неравномерных текущих платежах
Инвестиция выгодна, потому что 74,3 > 0.
На практике капитальные вложения могут осуществляться в объекты, период использования которых неограничен, например, ценные бумаги, земельный участок и другие. В этом случае схема инвестиционного процесса представляет собой бесконечный платежный ряд. Чистую дисконтированную стоимость в этом случае можно определить исходя из предположения определенной временной границы использования инвестиционного объекта, то есть определив t = n. Тогда формулу расчета чистой дисконтированной стоимости можно представить в виде:
(21)
Учитывая, что n → ∞, формула принимает вид:
(22)
Таким образом при осуществлении оценки эффективности методом чистой дисконтированной стоимости необходимо:
1) построить схему платежных потоков по инвестиционному процессу для принятого планового горизонта;
2) обосновать значение процентной ставки, которая позволяет учесть влияние фактора времени на ценность платежей;
3) выбрать формулу для расчета чистой дисконтированной стоимости в зависимости от характера текущих платежей и временного срока использования объекта;
4) выполнить расчеты чистой дисконтированной стоимости и сделать выводы о целесообразности осуществления капиталовложений в соответствии критерия метода.
Особенностью метода чистой дисконтированной стоимости является зависимость этого показателя от процентной ставки дисконтирования. При росте уровня процентной ставки проект может перейти из категории выгодных в категорию невыгодных. Исходя из динамичности процентной ставки в зависимости от ситуации на рынке капитала и условий финансирования проекта, неоднозначность данной характеристики можно считать недостатком метода чистой дисконтированной стоимости.
Вопросы для самоконтроля.
1. Раскройте сущность экономической категории «чистая дисконтированная стоимость».
2. Раскройте особенности формирования критерия метода чистой дисконтированной стоимости.
3. Каким закономерностям подчиняется изменение дисконтированной стоимости капитала при изменении процентной ставки дисконтирования?
4. В чем особенности определения чистой дисконтированной стоимости при неравномерных текущих платежах?
5. В чем специфика определения чистой дисконтированной стоимости при равномерных платежах по проекту?
Метод внутренней ренты
Этот недостаток отсутствует у показателя внутренней нормы прибыли (internal rate of return), характеризующий размер дохода на капитал, при котором наступает предел эффективности, то есть проект минимально выгодным. На графике зависимости ЧДС эта характеристика совпадает с ікр (рис. 18). Уровень внутренней нормы прибыли однозначно характеризует эффективность инвестиций, что упрощает его использование для принятия управленческих решений.
Критерий метода внутренней нормы доходности заключается в следующем: инновационный проект выгоден, если внутренняя норма прибыли (r, ВНП) не ниже процентной ставки дисконтирования, которую часто называют применительно к данному методу гарантированным минимальным доходом на капитал (і).
| . | (23) |
Рис. 18. Зависимость ЧДС от установленного уровня доходности
Таким образом, критерий метода внутренней ренты требует сравнения двух величин: минимального процента i, как установленного требования к инвестиционному объекту исходя из внешних условий, сложившихся на рынке капитала и внутреннего процента r, который вытекает из инвестиционных расчетов исходя из ожидаемой доходности капитала. Для использования критерия необходимо установить:
— уровень процентной ставки (i), установленной к конкретному проекту;
— уровень ожидаемой внутренней процентной ставки (r).
Установление требований к процентной ставке дисконтирования должно осуществляться исходя из стоимости капитала. Для этого в мировой практике наработан ряд методов:
— Метод СВСК (WACC), то есть средневзвешенной стоимости капитала;
— Метод оценки капитальных активов — МОКА (CAPM)
— Метод роста дивидендов;
— Метод «Доход на облигацию плюс премия за риск» и другие.
Рассмотрим упрощенно подход, который лежит в основе метода СВСК, учитывающий возможности использования различных источников финансирования инновационных объектов.
При финансировании исключительно собственным капиталом, необходимо рассматривать альтернативную возможность использования своих средств инвестором на рынке капитала. Поэтому минимальное требование процента, установленного при инвестировании, не может быть ниже процент (iдеп), выплачиваемой банками по вкладам, который сложился на рынке капитала:
| . | (24) |
ідеп –представляет собой нижнюю границу эффективности капитала. Причем, чем выше риск по проекту (особенно инновационному), тем выше устанавливается значение минимальной процентной ставки. Если обозначить надбавку, обусловленную степенью риска (іриск), то можно записать следующее условие:
| . | (25) |
Если финансирование осуществляется полностью заемным капиталом, то ориентиром для установления минимального процента является процентная ставка кредитора, под который предоставляется капитал (iкр):
| . | (26) |
При этом также требование кредитора представляет собой нижнюю границу эффективности. Формирование окончательного значения процентной ставки дисконтирования обусловлено также риском, связанным с конкретным проектом:
| . | (27) |
В случае если финансирование осуществляется частично собственным (СК) и частично заемным капиталом (ЗК), в качестве ориентира рассчитывается смешанная процентная ставка с учетом уровня использования каждого источника:
| . | (28) |
Размер внутренней ренты может устанавливаться различными методами. Рассмотрим графический подход. При его использовании нужно исходить из условия, что внутренней рентой является значение процента, при котором дисконтированная стоимость доходов совпадает со стоимостью затрат по конкретному проекту. Таким образом, расчет выполняется исходя из приравнивания критериев метода чистой дисконтированной стоимости и метода внутренней нормы прибыли. Чтобы определить внутреннюю ренту исходя из сравнения критериев, можно рассмотреть простой пример, который характеризуется таким численным рядом:
-100 108 д. ед.
0 1 годы
Рис. 19 Исходные данные для расчета динамики ЧДС
Проверим методом чистой дисконтированной стоимости, как будет меняться эффективность проекта при изменении процентной ставки (i). Для этого зададим значение процентной ставки (i) трижды:
i = 0,06 → ЧДС = 108 · 0,943396 — 100 = +1,89 д. ед.
i = 0,08 → ЧДС = 108 · 0,925926 — 100 = 0 д. ед.
i = 0,10 → ЧДС = 108 · 0,909091 — 100 = -1,83 д. ед.
Из приведенных расчетов ясно, что внутренняя рента этого проекта составляет 8%, так как именно при этом значении чистая дисконтированная стоимость равна нулю, то есть наступает предел эффективности инвестиций. Рассмотрим параллельно критерии дисконтированной стоимости капитала и внутренней нормы прибыли (таблица 5).
Таблица 5
Критерии метода чистой дисконтованной стоимости и метода внутренней ренты
| Альтернативная процентная ставка | Оценка эффективности | Оценка эффективности в соответствии с критериями |
| i = 0,06 | Выгодно | ЧДВ > 0 r > i |
| i = 0,08 | Минимально выгодно | ЧДВ = 0 r = i |
| i = 0,10 | Невыгодно | ЧДВ < 0 r < i |
Как видно из таблицы, при процентной ставке i = 0,06 получаем положительное значение дисконтированной стоимости капитала. Это означает, что инвестор не только компенсирует потраченные средства с учетом фактора времени, но и получит доход в размере приведенной стоимости капитала. При этом внутренняя процентная ставка превышает размер процента дисконтирования.
При значении i = 0,08 инвестор только вернет потраченные средства с учетом фактора времени. Дисконтированная стоимость капитала равна нулю. Внутренняя рента равна проценту дисконтирования.
При повышении процентной ставки до i = 0,10 проект невыгоден. Дисконтированная стоимость капитала меньше нуля. Внутренняя рента ниже процента дисконтирования.
Особое значение имеет второй пункт рассматриваемого примера. Он характеризует условие предельной выгодности проекта. При этом ЧДС = 0, r = i.
Рассмотрим графически данный пример, построим график (рис. 20), исходя из полученных значений приведенной стоимости капитала:
Рис. 20. Зависимость дисконтированной стоимости капитала от процентной ставки
На рисунке видно, что линия дисконтированной стоимости капитала пересекает ось абсцисс в точке i = 0,08. В этой точке значение внутренней процентной ставки и требования процента доходов на капитал совпадают, а дисконтированная стоимость капитала равна нулю. Таким образом, процентная ставка, при которой дисконтированная стоимость капитала равна нулю, является внутренней нормой прибыли инвестиции (это положение соответствует определению внутренней ренты).
Одним из аналитических методов расчета внутренней ренты является метод полинома. Исходным условием его использования также является критерий дисконтированной стоимости капитала:
| , | (29) |
де Пj –платежи по проекту (затраты, доходы либо капитальные затраты и чистые денежные потоки) в j-м периоде.
Использование метода полинома рассмотрим на примере проекта, который характеризуется следующим численным рядом:
-100 10 10 100 д. ед.
0 1 2 3 годы
Рис. 21 Исходные данные для расчета эффективности методом полинома
Для определения внутренней нормы прибыли составим уравнения чистой дисконтированной стоимости:
В случае, когда i = r уравнение имеет вид:
Для упрощения принимаем, что 1+r=х. Уравнение принимает следующий вид:
Умножим уравнение на х3:
Это уравнение представляет собой полином третьей степени. Его можно решить методом касательных, согласно которому значение неизвестного параметра устанавливается путем поэтапного подбора. На первом этапе оно задается произвольно. На следующих этапах уточнение осуществляется по формуле:
| . | (30) |
Количество этапов определяется обеспечением требования хi+1 = хi .
В качестве отправной точки примем х = 1,1. Значения составляющих формулы 30 соответственно характеристик данного проекта определяется следующим образом:
Первая итерация:
Вторая итерация:
Третья итерация:
В связи с тем, что полученные в результате третьей итерации значение х2 почти не отличается от значения х3, принимаем как итоговый результат х = 1,068860179. Таким образом, внутренняя норма прибыли составляет 6,89%. Для оценки достоверности полученного результата используем критерий дисконтированной стоимости, соответственно которого при значении процентной ставки на уровне внутренней ренты этот показатель равен нулю.
і = r
Как видно из расчетов при i = r дисконтированная стоимость капитала равна нулю, что подтверждает правильность полученного значения внутренней нормы прибыли.
Другим методом определения уровня внутренней нормы прибыли является метод хорды. На рис. 22 приведена зависимость чистой дисконтированной стоимости от процентной ставки. Задача касается определения координат точки пересечения кривой К1К2 с горизонтальной координатной осью. В случае, когда эта линия будет минимально короткой, эти координаты практически совпадают с координатами точки М, находящейся в месте пересечения с горизонтальной координатной осью прямой линии К1К2, которая представляет собой хорду.
Рис. 22. Зависимость ЧДС от процентной ставки дисконтирования
Известным в математике является уравнение хорды, которое в общем виде отражает взаимосвязь координат трех точек:
| . | (31) |
С учетом сущности анализируемых показателей, это уравнение можно представить в следующем виде:
| . | (32) |
Подставил известны координаты точки М (ЧДС = 0; i = r), получим следующее:
| . | (33) |
Преобразуем уравнение путем возведения его в минус первую степень:
| | ∙ (-ЧДC1); | (34) | |
| . | (35) |
В результате получаем формулу расчета внутренней нормы прибыли:
| . | (36) |
Расчет внутренней нормы прибыли методом хорды осуществляется по следующим этапам:
1. Составить уравнения расчета чистой дисконтированной стоимости инвестиции, которая подвергается анализу.
2. Произвольно задать два значения процентной ставки i1 и i2, предполагая, что значение внутренней нормы прибыли находится в интервале между ними.
3. Рассчитать значение чистой дисконтированной стоимости для заданных значений i1 и i2. Если ЧДC1> 0, а ЧДС2 <0, то переходим к следующему этапу. Если это требование не выполняется, то необходимо скорректировать i1 или i2 и повторно выполнить расчеты.
4. Определить величину внутренней нормы прибыли используя формулу 36.
5. Сделать вывод об эффективности каждого варианта инвестирования в соответствии с критерием.
6. Выбрать наиболее выгодный вариант инвестирования, исходя из требования максимизации значение внутренней ренты.
Рассмотрим использование метода хорды для расчета внутренней нормы прибыли в условиях предыдущего примера: -100, 10, 10, 100.
Зададим два значения процентной ставки: і1 = 5 %; і2 = 10 %. Рассчитаем соответствующие значения чистой дисконтированной стоимости:
і1 = 5 %
i2 = 10%
r = 6,99 %
Отклонение полученного знания от предыдущего метода определения внутренней ренты обусловлено погрешностями расчета. Следует указать, что чем короче будет хорда, тем выше точность показателя.
Вопросы для самоконтроля.
1. Раскройте сущность экономической категории «внутренняя рента».
2. Сформулируйте и обоснуйте критерий метода внутренней ренты.
3. Проанализируйте зависимость чистой дисконтированной стоимости от установленного уровня доходности.
4. Раскройте факторы формирования процентной ставки дисконтирования.
5. Раскройте факторы формирование внутренней процентной ставки по проекту.
6. Опишите процедуру определения эффективности инвестиционного проекта методом внутренней ренты.
Литература для самостоятельного изучения материала
5. Балабанов И.Т. Инновационный менеджмент : учебное пособие / И. Т. Балабанов. — СПб. : Питер, 2000. – 208 с.
6. Бланк И.А. Основы инвестиционного менеджмента / И.А. Бланк. – 2-е изд., перераб. и доп. – К.: Эльга: Н ка-Центр, 2008. – 672 с.
7. Богатин Ю. В. Инвестиционный анализ, Учеб.пособие для вузов, Всерос. заоч.финансово-экон.ин-т . — М. : ЮНИТИ ; М.: ДАНА, 2010. – 286 с.
8. Вахрин П.И. Инвестиции: (Практ. задачи и конкретные ситуации): Учеб. пособие для вузов. – М.: Дашков и К., 2008. – 212 с.
9. Зимин И.А. Реальные инвестиции, Учеб.пособие . — М. : ЭКМОС, 2000 . — 304с.
12. Інвестування: Навч.-метод. посіб. для самост. вивч. дисц. / Пересада А.А,, Смірнова О.О., Онікієнко С.В. – К.: КНЕУ, 2011. – 251 с.
13. Кожухар В.М. Инновационный менеджмент : практикум / В. М. Кожухар ; В.М. Кожухар. — М. : Изд.-торг. корпорация «Дашков и К», 2010. — 200с.
14. Марголин А.М., Быстряков А.Я. Экономическая оценка инвестиций: Учебник для вузов и техникумов. – М.: ЭКМОС, 2009. – 204 с.
15. Маховикова Г. А. Инвестиционный процесс на предприятии, Учеб.пособие для вузов . — СПб.: Питер, 2001 . — 176с.
16. Орлова Е.Р. Инвестиции: Курс лекций. – М.: Омега-Л, 2003. — 192с.
18. Решецкий В.И. Экон. Анализ и расчет инвестиционных проектов: Учеб. пособие. – Калининград: Янтарный сказ, 2004. – 477 с.
19. Савчук А.В. Анализ эффективности инвестиционных проектов и экономических условий их реализации / А.В.Савчук; НАН Украины. – Одесса: ИПРЭЭИ, 2009. – 176 с.
21. Филин С.А. Инвестиционные возможности экономики и решение проблемы неплатежей. – М.: ООО «Фирма Благовест–В”, 2009. – 512 с.
22. Хобта В.М. Управління інвестиціями: навчальний посібник. – Донецьк: ДонНТУ, 2009. – 394 с.
⇐ Предыдущая123
Дата добавления: 2017-03-12; просмотров: 2283 | Нарушение авторских прав | Изречения для студентов
В статье подробно расскажем про дисконтирование денежных потоков, формулу расчета и анализа в Excel.
Содержание
- Дисконтирование денежных потоков. Определение
- Как рассчитать коэффициент дисконтирования?
- Дисконтирование денежных потоков. Формула расчета
- Расчет нормы дохода (r) для дисконтирования денежных потоков
- Пример расчета дисконтированного денежного потока в Excel
- Методы инвестиционного анализа, использующие дисконтированные денежные потоки
- Достоинства и недостатки показателя DCF дисконтирования денежных потоков
Дисконтирование денежных потоков. Определение
Дисконтирование денежных потоков (англ. Discounted cash flow, DCF, дисконтированная стоимость) – это приведение стоимости будущих (ожидаемых) денежных платежей к текущему моменту времени. Дисконтирование денежных потоков основывается на важном экономическом законе убывающей стоимости денег. Другими словами, со временем деньги теряют свою стоимость по сравнению с текущей, поэтому необходимо за точку отсчета взять текущий момент оценки и все будущие денежные поступления (прибыли/убытки) привести к настоящему времени. Для этих целей используют коэффициент дисконтирования.
Как рассчитать коэффициент дисконтирования?
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут Коэффициент дисконтирования используется для приведения будущих доходов к текущей стоимости за счет перемножения коэффициента дисконтирования и потоков платежей. Ниже показана формула расчета коэффициента дисконтирования: где: r – ставка дисконтирования, i – номер временного периода.
Дисконтирование денежных потоков. Формула расчета
где: DCF (Discounted cash flow) – дисконтированный денежный поток; CF (Cash Flow) – денежный поток в период времени I; r – ставка дисконтирования (норма дохода); n – количество временных периодов, по которым появляются денежные потоки. Ключевым элементов в формуле дисконтирования денежных потоков является ставка дисконтирования. Ставка дисконтирования показывает, какую норму прибыли следует ожидать инвестору при вложении в тот или иной инвестиционный проект. Ставка дисконтирования использует множество факторов, которые зависят от объекта оценки, и может в себя включать: инфляционную составляющую, доходность по безрисковым активам, дополнительную норму прибыли за риск, ставку рефинансирования, средневзвешенную стоимость капитала, процент по банковским вкладам и т.д.
Расчет нормы дохода (r) для дисконтирования денежных потоков
Существует достаточно много различных способов и методов оценки ставки дисконтирования (нормы дохода) в инвестиционном анализе. Рассмотрим более подробно достоинства и недостатки некоторых методов расчета нормы доходности. Данный анализ представлен в таблице ниже.
|
Методы оценки ставки дисконтирования |
Достоинства |
Недостатки |
| Модели CAPM | Возможность учета рыночного риска | Однофакторность, необходимость наличия обыкновенных акций на фондовом рынке |
| Модель Гордона | Простота расчета | Необходимость наличия обыкновенных акций и постоянных дивидендных выплат |
| Модель средневзвешенной стоимости капитала (WACC) | Учет нормы дохода как собственного, так и заемного капитала | Сложность оценки доходности собственного капитала |
| Модель ROA, ROE, ROCE, ROACE | Возможность учета рентабельности капиталов проекта | Не учет дополнительных макро, микро факторов риска |
| Метод E/P | Учет рыночного риска проекта | Наличие котировок на фондовом рынке |
| Метод оценки премий на риск | Использование дополнительных критериев риска в оценке ставки дисконтирования | Субъективность оценки премии за риск |
| Метод оценки на основе экспертных заключений | Возможность учесть слабоформализуемые факторы риска проекта | Субъективность экспертной оценки |
Вы можете более подробно узнать про подходы в расчете ставки дисконтирования в статье «Ставка дисконтирования.10 современных методов оценки».
Пример расчета дисконтированного денежного потока в Excel
Для того чтобы рассчитать дисконтированные денежные потоки необходимо по выбранному временному периоду (в нашем случае годовые интервалы) расписать подробно все ожидаемые положительные и отрицательные денежные платежи (CI – Cash Inflow, CO – Cash Outflow). За денежные потоки в оценочной практике берут следующие платежи:
- Чистый операционный доход;
- Чистый поток наличности за исключением затрат на эксплуатацию, земельного налога и реконструирования объекта;
- Облагаемая налогом прибыль.
В отечественной практике, как правило, используют период 3-5 лет, в иностранной практике период оценки составляет 5-10 лет. Введенные данные являются базой для дальнейшего расчета. На рисунке ниже показан пример ввода первоначальных данных в Excel.
Дисконтированный денежный поток (DCF) расчет в Excel
На следующем этапе рассчитывается денежный поток по каждому из временных периодов (колонка D). Одной из ключевых задач оценки денежных потоков является расчет ставки дисконтирования, в нашем случае она составляет 25%. И была получена по следующей формуле: Ставка дисконтирования = Безрисковая ставка + Премия за риск За безрисковую ставку была взята ключевая ставка ЦБ РФ. Ключевая ставка ЦБ РФ на настоящий момент составляет 15% и премия за риски (производственные, технологические, инновационные и др.) была рассчитана экспертно на уровне 10%. Ключевая ставка отражает доходность по безрисковому активу, а премия за риск показывает дополнительную норму прибыли на существующие риски проекта. Более подробно узнать про расчет безрисковой ставки можно в следующей статье: «Безрисковая ставка доходности. 5 современных методов расчета» После необходимо привести полученные денежные потоки к первоначальному периоду, то есть умножить их на коэффициент дисконтирования. В результате сумма всех дисконтированных денежных потоков даст дисконтированную стоимость инвестиционного объекта. Формулы расчета будут следующие: Денежный поток (CF) = B6-C6 Дисконтированный денежный поток (DCF) = D6/(1+$C$3)^A6 Суммарный дисконтированный денежный поток (DCF) = СУММ(E6:E14)
Дисконтирование денежных потоков, пример оценки в Excel
В результате расчета мы получили дисконтированную стоимость всех денежных потоков (DCF) равную 150 981 руб. Данный денежный поток имеет положительное значение, это свидетельствует о возможности дальнейшего анализа. При проведении инвестиционного анализа необходимо сопоставить итоговые значения дисконтированного денежного потока по различным альтернативным проектам, это позволит проранжировать их по степени привлекательности и эффективности в создании стоимости.
Методы инвестиционного анализа, использующие дисконтированные денежные потоки
Следует заметить, что дисконтированный денежный поток (DCF) в своей формуле расчета сильно походит на чистый дисконтированный доход (NPV). Главное отличие заключается во включении первоначальных инвестиционных затрат в формулу NPV. Дисконтированный денежный поток (DCF) используется во многих методах оценки эффективности инвестиционных проектов. Из-за того, что данные методы используют дисконтирование денежных потоков, их называют динамическими.
- Динамические методы оценки инвестиционных проектов
- Чистый дисконтированный доход (NPV, Net Present Value)
- Внутренняя норма прибыли (IRR, Internal Rate of Return)
- Индекс прибыльности (PI, Profitability index)
- Эквивалент ежегодной ренты (NUS, Net Uniform Series)
- Чистая норма доходности (NRR, Net Rate of Return)
- Чистая будущая стоимость (NFV, Net Future Value)
- Дисконтированный срок окупаемости (DPP, Discounted Payback Period)
Более подробно узнать про методы расчета эффективности инвестиционных проектов вы можете в статье «6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI». Помимо только дисконтирования денежных потоков существую более сложные методы, которые в дополнение учитывают реинвестирование денежных платежей.
- Модифицированная чистая норма рентабельности (MNPV, Modified Net Rate of Return)
- Модифицированная норма прибыли (MIRR, Modified Internal Rate of Return)
- Модифицированный чистый дисконтированный доход (MNPV, Modified Present Value)
Достоинства и недостатки показателя DCF дисконтирования денежных потоков
+) Использование ставки дисконтирования является несомненным достоинством данного метода, так как позволяет привести будущие платежи к текущей стоимости и учесть возможные факторы риска при оценке инвестиционной привлекательности проекта. -) К недостаткам можно отнести сложность прогнозирования будущих денежных потоков по инвестиционному проекту. К тому же трудно отразить в ставке дисконтирования изменения внешней среды. Резюме Дисконтирование денежных потоков является основой для расчета многих коэффициентов оценки инвестиционной привлекательности проекта. Мы разобрали на примере алгоритм расчета дисконтированных денежных потоков в Excel, их существующие достоинства и недостатки. С вами был Иван Жданов, спасибо за внимание.
к.э.н. Жданов Иван Юрьевич

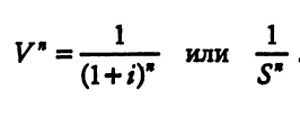

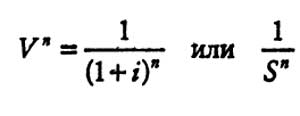
Добавить комментарий